Relation 2 Verticalline Test 3 Function Notation 4 Discrete Data 5 Continuous Data

Vertical Line Test

Vertical line test is helpful to find if the given equation represents a function or not. The vertical line test states that a vertical line needs to cuts the graph of a function(equation) at only one point, for it to represent a function. If the graph of the equation represented in the coordinate axis, is cut by the vertical line at more than one point, then the graph is not a function.

The vertical line cuts the graph of a function at only one point, and hence it has only one y value(codomain) for the x value(domain). Let us learn more about graphing a vertical line test, and how to apply the vertical line test, with the help of examples, FAQs.

1.	What Is Vertical Line Test?
2.	Graph of Vertical Line Test
3.	How to Apply Vertical Line Test?
4.	Examples on Vertical Line Test
5.	Practice Questions
6.	FAQs on Vertical Line Test

What Is Vertical Line Test?

A vertical line test helps to find if the graph is a function or not. The vertical line in a coordinate system represents a set of infinite points having the same x coordinate values and different y coordinate values for each of its points. The vertical line is drawn parallel to the y-axis, if it cuts the curve at one distinct point then it has one y-value for the given x value and it follows the basic definition of a function.

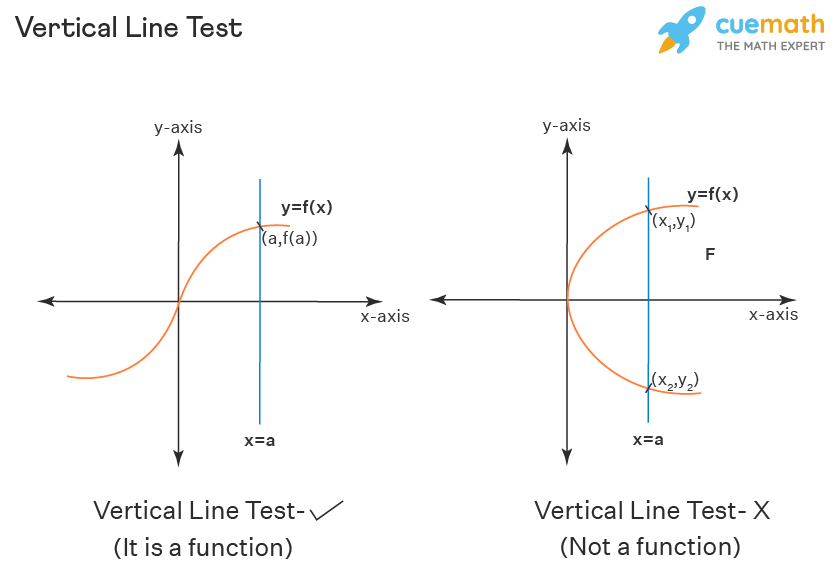
The vertical line test is helpful in knowing if a relation is a function or not. The vertical line test satisfies the definition of a function: for every domain x value, there is only one range y value for the function. The vertical line x = a, if it cuts the curve y = f(x) at only one point (a, f(a)), then such a curve y = f(x) represents a function.

A vertical line is supposed to cut the curve at only one point, for the curve to represent a function. And if the vertical line x = a is cutting the graph y = f(x) at more than one point, ie... at two points such as (x, y₁), (x, y₂), then it is having different y values for the same x-value. Thus each domain has more than one codomain value and it contradicts the basic definition of a function, and the curve y = f(x) does not represent a function.

A function is expected to have a unique range for each of its domains, and if the input has more than one output, then it is not considered a function: this can be identified using the vertical line test. If a vertical line intersects the graph of the relation at only one point, then it is a function, and if it intersects at more than one point then the graph does not represent a function.

Graph of Vertical Line Test

A graph of a vertical line helps to easily identify if the given equation y = f(x) represents a function or not. In each of the graphs, we can conclude by a quick observation if the vertical line is cutting the curve at one point or more than one point. If the line is cutting the curve more than once, then it does not represent the graph of a function. For a function, the vertical line needs to cut the curve at only one point.

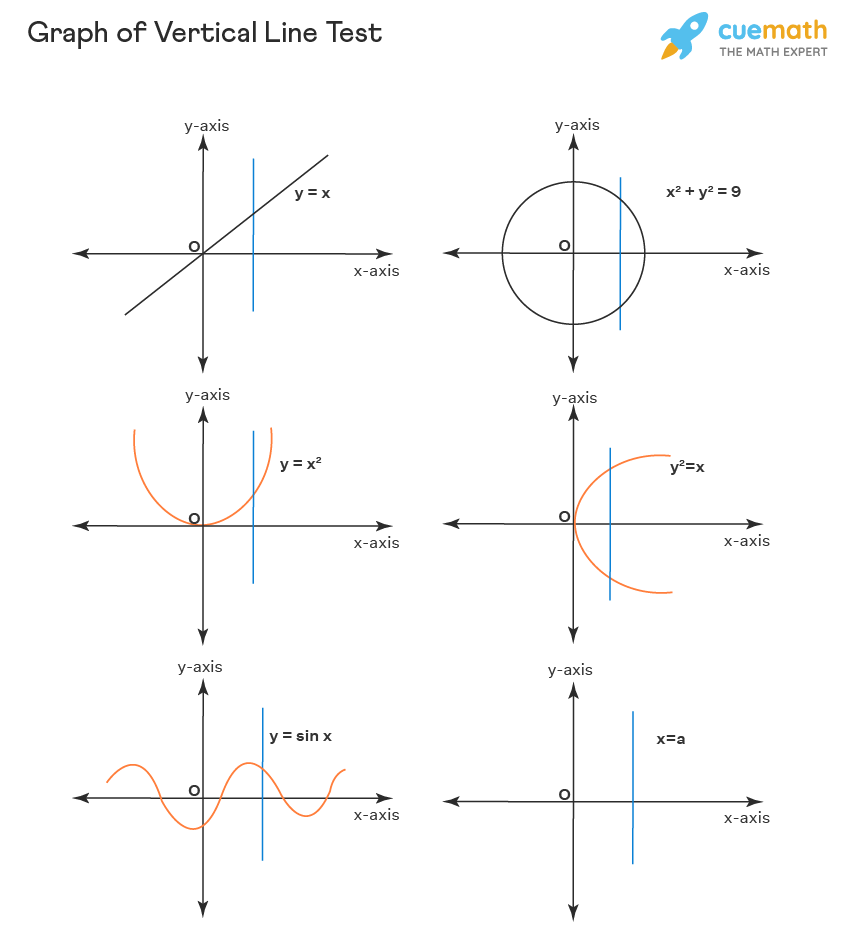
In the above graph, the three graphs towards the left have the vertical lines cutting it at only one point, and hence they represent a function, and the three graphs towards the right do not represent the function as the vertical line cuts the graph at two points. Let us check the examples of a few of the equations which represent a function, and a few equations which do not represent functions.

Equations representing functions: y = x, y = x², y = 3, y = |x|, y = Sinx, y = x³, y = \(3\sqrt x\),

Equations which do not represent functions: x = y², x² + y² = 9, x = 4, y = \(\sqrt x\)

We can draw the graph for each of these equations, and use the vertical line test, to check if they are a function or not a function.

How To Apply Vertical Line Test?

The following sequence of steps are needed to be followed to apply the vertical line test, to find if the given expression is a function or not. There are two methods of applying the vertical line test. It can be applied geometrically or algebraically. Let us consider a function y = f(x) and the vertical line having the equation x = a.

Geometrically: Draw the graph of y = f(x), with respect to the coordinate axis. Now draw the line x = a, and observe the number of places it cuts the curve y = f(x). If this vertical line cuts the curve at more than one place, then the curve does not represent a function. If the vertical line cuts the curve at only one point which is (a, f(a)), then the curve y = f(x) represents a function.

Algebraically: The equation of a vertical line is x = a and substituting it in the equation of a curve y = f(x), we get y = f(a). If we get more than one value for y, then it proves that the equation y = f(x) does not represent a function. Further if we get only a single value for y, on substituting x = a in y = f(x), then y = f(x) represents a function.

☛ Related Topics

• Equation of Line Parallel to Y-Axis
• Equation of Line Parallel to X-Axis
• Slope
• Equation of Line
• Point Slope Form

Examples on Vertical Line Test

1. Example 1: Find if the equation y = \(\sqrt 2x\) + 5 represents a function or not. Use the vertical line test to prove if it is a function or not.

   Solution:

   The given expression is y = \(\sqrt 2x\) + 5. We need to check for this expression using the vertical line test.

   Let us consider a vertical line having the equation x = 8. Let us substitute x = 8 in the expression y = \(\sqrt 2x\) + 5.

   y = \(\sqrt 2(8)\) + 5

   y = \(\sqrt {16}\) + 5

   y = + 4 + 5

   y = +4 + 5, and y = -4 + 5

   y = +9, y = +1

   Hence the line x = 8 cuts the curve y = \(\sqrt 2x\) + 5 at two points (8, 1), and (8, 9).

   Therefore using the vertical line test we can prove that the curve y = \(\sqrt 2x\) + 5 does not represent a function.

2. Example 2: Using the vertical line test, check if the expression x² + 3x - 7y + 4 = 0 represents a function or not.

   Solution:

   The given expression is x² + 3x - 7y + 4 = 0.

   We can write it as y = 1/7.(x² + 3x + 4)

   To check for vertical line test, let us consider a vertical line x = 2. We need to find the number of times this vertical line cuts the graph of the above curve, and hence let us substitute x = 2 in the above equation.

   y = 1/7.(2² + 3(2) + 4)

   y = 1/7.(4 + 6 + 4)

   y = 14/7

   y = 2

   Here we have obtained only one value of y, and the line x = 2 cuts the curve x² + 3x - 7y + 4 = 0 at only one point, (2, 2), and hence we can conclude that the equation of the curve represents a function.

   Thus with the help of the vertical line test, we can successfully conclude that the given equation represents a function.

go to slidego to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

Practice Questions on Vertical Line Test

go to slidego to slide

FAQs on Vertical Line Test

What Is Vertical Line Test In Geometry?

The vertical line test is useful to find if a curve represents a function or not. The vertical line is parallel to the y-axis and is represented as x = a. If the vertical line cuts the curve y = f(x) at one distinct point, then the curve represents a function, and if it cuts at more than one distinct point, then it does not represent a function.

How To Apply Vertical Line Test?

The vertical line test can be applied geometrically or algebraically. Geometrically, If the vertical line x = a cuts the graph of the curve y = f(x) at one point, then the graph represents a function, and if it cuts the curve at more than one point, then it does not represent a function. Algebraically, if the point x = a gives a unique value for y = f(x0, then it is a function, and if it gives more than one value, then the equation does not represent a function.

What Is The Formula Of Vertical Line Test?

The formula of vertical line test includes the substitution of x = a in y = f(x), if it gives a single unique value of y = f(a), then it is a function, and if it gives more than one value, then it does not represent a function.

What Is The Importance Of Vertical Line Test?

The vertical line test is important since it helps to easily find if a curve represents a function or not. Through a visual representation, we can easily find if the curve is a function or not. If the vertical line cuts the curve at one point then it is a function, and if it cuts at more than one point then it does not represent a function.

What Can be Said About A Relation From The Vertical Line Test?

The relation relates the x and y values, or the domain and codomain values with the equation y = f(x). If the vertical line cuts the graph of the relation y = f(x) at one distinct point then it is a function, and if it cuts the graph at more than one point then it is not a function.

Can We Find The Domain And Range Of A Function Using Vertical Line Test?

The vertical line test is helpful to easily find the domain and range of the function. If the curve y = f(x) is a function, then the vertical line x = a cuts the graph of the function at only one point, and x = a is the domain and y = f(a) is the codomain of the function.

What Is The Difference Between Vertical Line Test And Horizontal Line Test?

The vertical line test helps to find it a given curve represents a function or not. If the vertical line cuts the graph of the equation at only one point, then it is a function, and if cuts the graph of the function at more than one point, then it does not represent a function.

The horizontal line test helps to find if a function is a injective function or not. If a horizontal line cuts the graph of the function at only one point then it is an injective function, and also the function has a unique inverse. If the horizontal line cuts the function at more than one point, then it has same codomain values for different domain values, and the function is not an injective function.

balketheryinithou.blogspot.com

Source: https://www.cuemath.com/algebra/vertical-line-test/